投影变换与矩阵推导

前言

本文主要目的是推导投影矩阵。曾经刚了解投影矩阵的时候，面对网上搜到的各种各样的推导非常头疼，因为他们推导前提条件和结果都不一样。本文会在非常明确的前提下推导出投影矩阵，并简略说明Games 101和《Unity Shader入门精要》中的投影矩阵的不同之处。

首先明确一点，推导投影矩阵时假设的前提条件不一样时（比如：视锥体位置、左手系或右手系、摄像机看向z轴正方向还是负方向、已知的参数等），推导出的结果会有所不同，。本文的推导过程假设使用右手系，摄像机看向z轴负方向，已知的参数和视锥体位置另有说明。

正交投影

首先假设视锥体近平面位于z = 0处，则视锥体远平面位于z = n-f处（z < 0），则

假设近平面的中心位于坐标原点，设视锥体中x和y的取值范围如下：

在视锥体内有一点位于视锥体内，如下图所示。

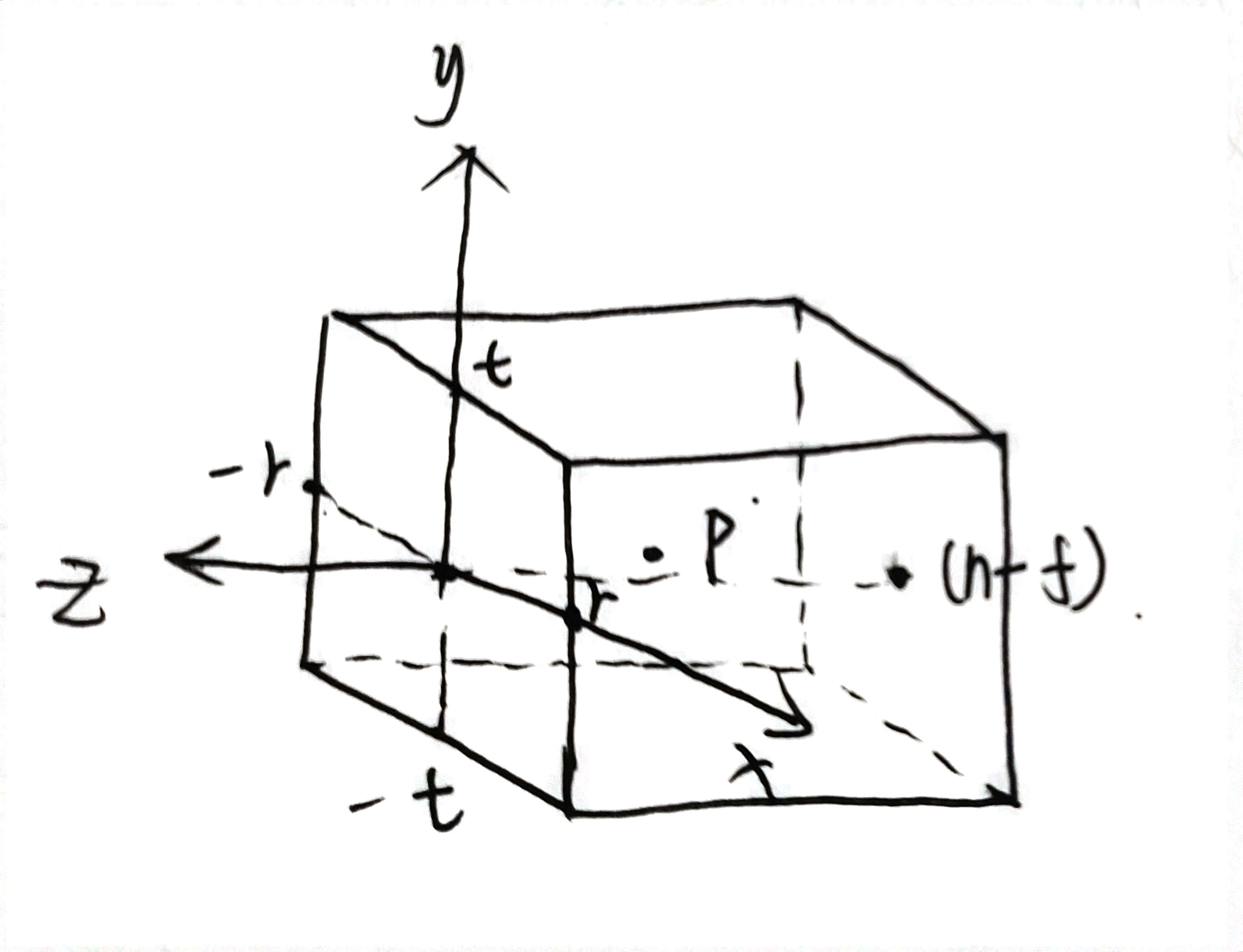
我们的目标是将视锥体内任意一点的坐标变换至，变换后的示意图如下：

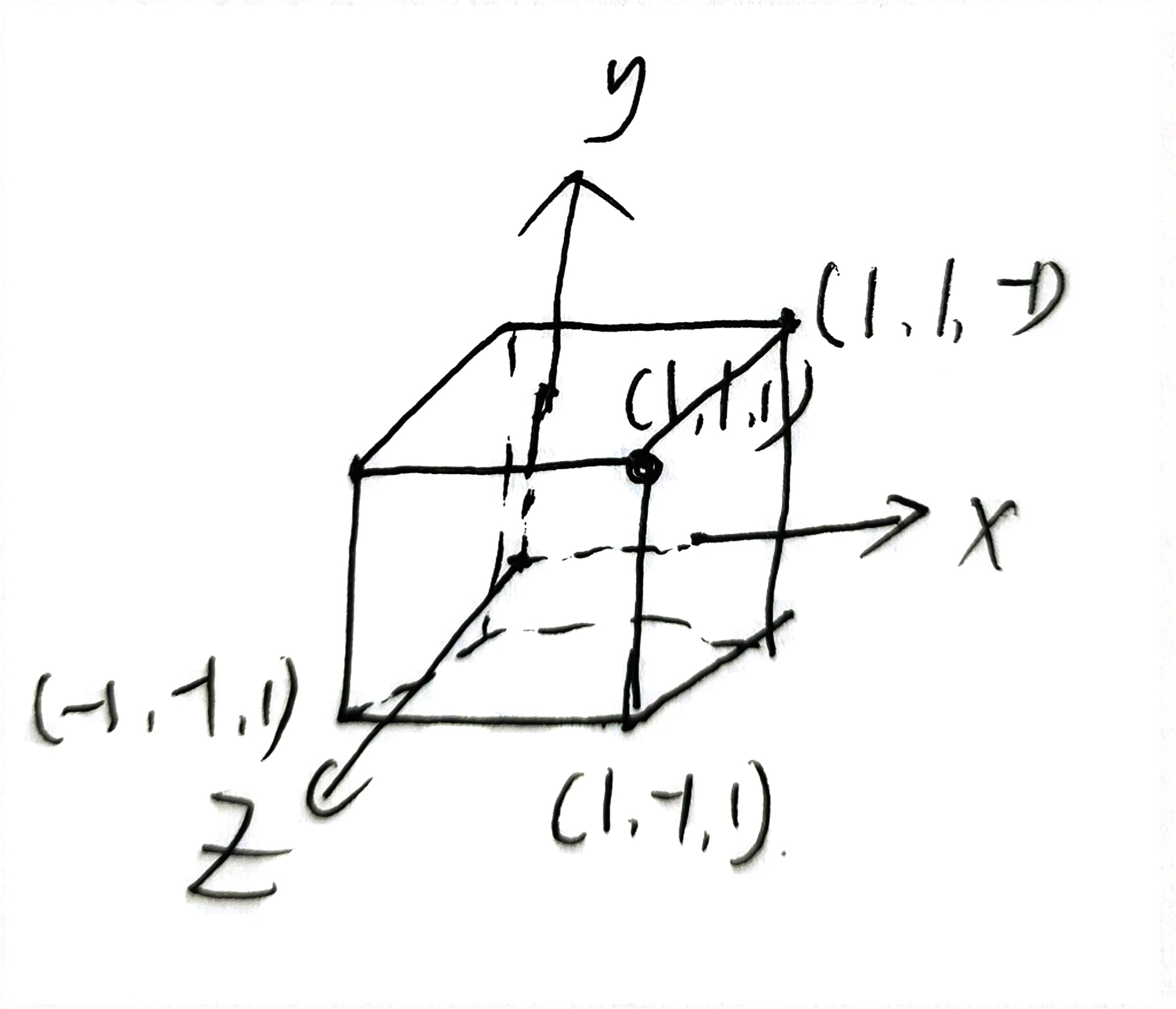
为了达到这个目的，我们需要将点P的坐标分别进行缩放：

则对应的矩阵为：

在Unity中，我们一般使用另外的参数来描述正交相机，即：， ，则，于是投影矩阵可以表示为：

注意，这个正交投影矩阵与Games 101和《Unity Shader入门精要》中的正交投影矩阵都不相同。

与本节的假设相比，《Unity Shader入门精要》第81页中的正交投影矩阵假设原始视锥体的近平面并没有位于处，而是位于处，**即对于原始视锥体中的任意一点，**，其正交投影矩阵如下：

与本节的假设相比，Games 101中的投影矩阵的推导，假设视锥体位于任何位置（但视锥体始终与坐标轴平行），具体推导可以见:GAMES101-现代计算机图形学入门-闫令琪

透视投影

对于透视投影，其视锥体为一个平截头体（frustum），我们先考虑将其”压缩”，即保持近平面不变，将其”压缩”为一个立方体，然后利用透视投影的方法得到结果。

假设平截头体所在四棱锥的顶尖位于坐标原点，朝向z轴负方向，并且关于x轴和y轴对称，有一点位于视锥体内，如下图所示：

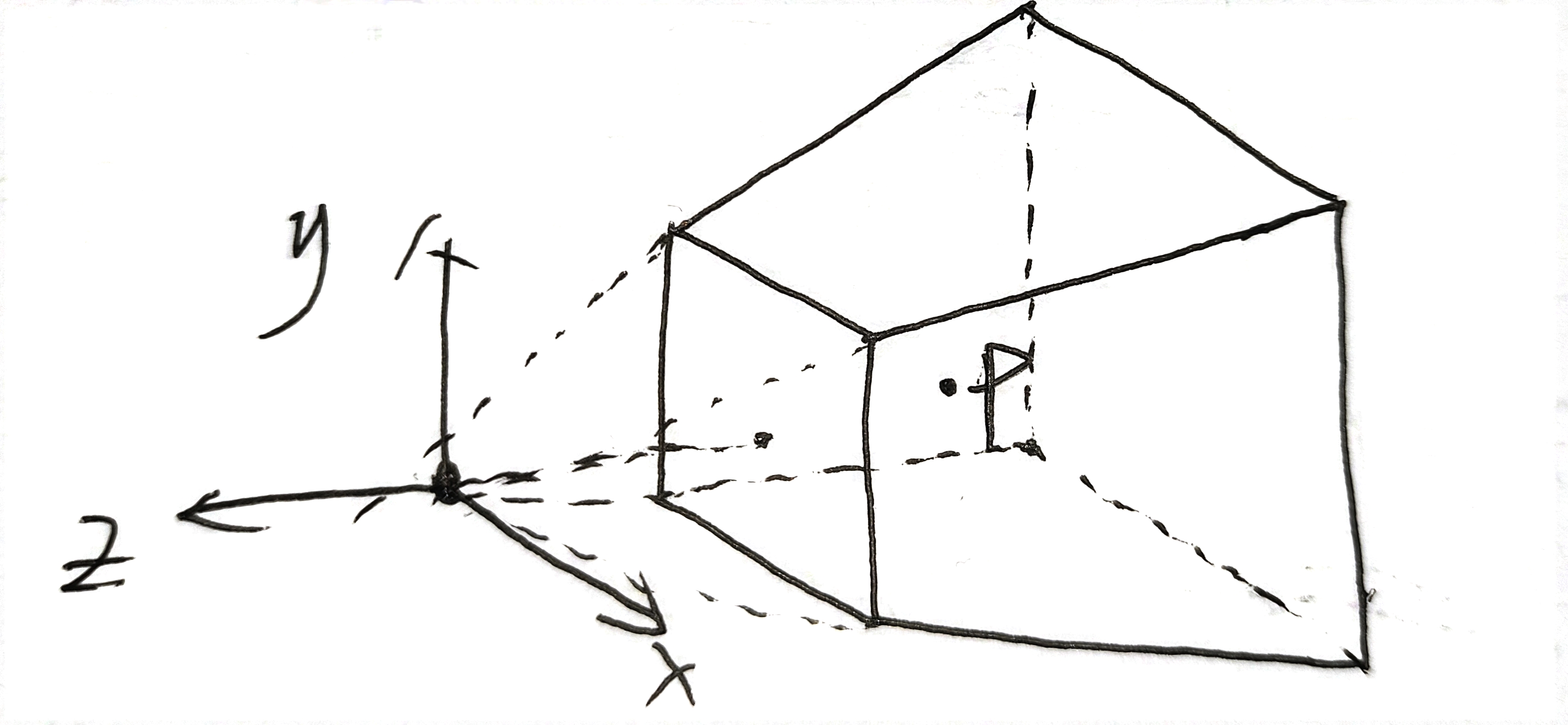
首先考虑点的坐标，我们从下往上去看（或者从上往下看，一样的），如下图所示：

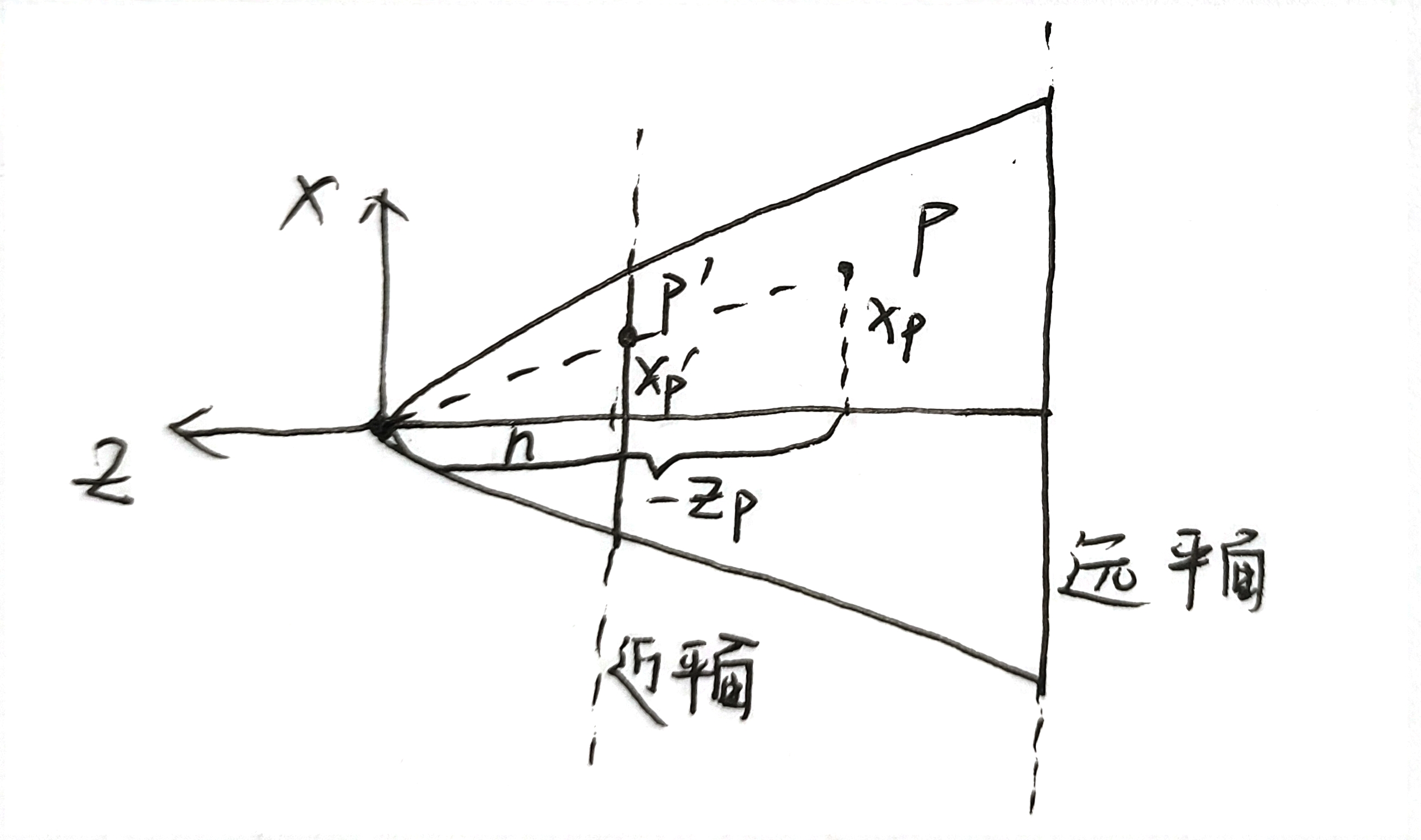
则可以很容易的由相似三角形得到变换后的坐标

同理可得（懒得画图了）：

我们暂时先不处理。由于式子中含有，无法直接写在矩阵当中，所以接下来需要经过一些特别的处理。我们知道，对于齐次坐标：

这两个齐次坐标表示三维空间中的同一个点。如果我们某一次计算的结果是后一种，则”隐含了”接下来要除以n的操作。因此我们得到如下矩阵：

*=

这个矩阵已经可以完美描述和的变换了，对于，我们无法简单的找到公式，但是我们发现对于近平面和远平面内的点，变换后的，而位于视锥体内部的点则不一定。并且与和无关，于是我们可以根据近平面和远平面上的点列出式子。

对于近平面，其：

* = ,即： * =

对于远平面，其

* = ,即： * =

解这个方程组即可得到：

的值与Games 101中推导出的值不同（大概是因为他们假设，与我们的假设不同）。

于是可得矩阵

经过透视投影矩阵一投影后，原视锥体由平截头体变为一个立方体，坐标取值范围为，，，再次对其应用正交投影矩阵二:

* =

接下来是换参数的问题。在Unity中，透视相机由、、和定义

所以最终的透视投影矩阵可以写为

透视投影矩阵三与《Unity Shader入门精要》第79页的矩阵相同。

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 YuJie-Ding@qq.com